Skip to content

决策树与随机森林

省流

### **决策树与随机森林**

**1. 核心作用**

- **决策树**：通过树状规则划分数据，解决分类/回归问题，**可解释性强**（可视化规则）。  
- **随机森林**：集成多棵决策树，提升预测精度和泛化能力，**抗过拟合**。

**2. 能解决的问题**

- **分类问题**：用户流失预测、垃圾邮件识别、疾病诊断（如是否患糖尿病）。  
- **回归问题**：房价预测、销量预估、能源需求分析。  
- **特征重要性分析**：识别关键影响因素（如影响用户购买的核心变量）。  
- **异常检测**：通过树的分割规则识别离群点。

**3. 典型应用场景**

- **金融**：信用评分、欺诈检测  
- **医疗**：患者风险分层、治疗方案选择  
- **电商**：用户行为分类（高/低价值客户）  
- **工业**：设备故障模式识别

**4. 常用方法**

- **决策树算法**：ID3（信息增益）、C4.5（增益率）、CART（Gini指数/均方误差）。  
- **随机森林优化**：Bagging（自助采样）、特征随机选择、OOB误差评估。  
- **扩展模型**：梯度提升树（GBDT）、XGBoost（高性能优化）。

**5. 使用建议**

- **数据要求**：可处理数值和类别特征，无需严格标准化（树模型对尺度不敏感）。  
- **调参重点**：树深度、叶子节点最小样本数（防过拟合）；森林中树的数量。  
- **结果解释**：用SHAP值、特征重要性图增强可解释性（尤其随机森林）。

---  
**简练总结**：决策树适合 **可解释性优先** 的简单问题；随机森林适合 **高精度、复杂数据** 场景，数学建模中常见于分类/回归赛题（如金融风控、医疗预测），需注意 **避免维度爆炸** 和 **计算效率** 权衡。

决策树

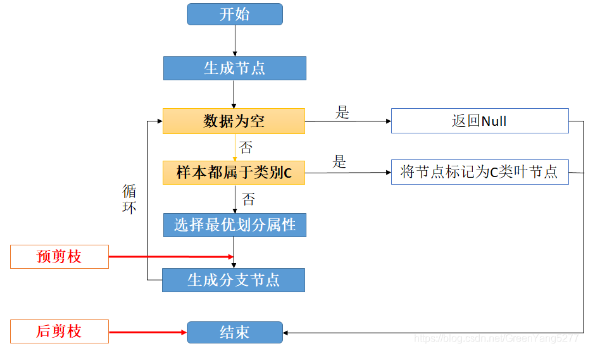
决策树：它是一种以树形数据结构来展示决策规则和分类结果的模型。分为 分类树和回归树 两种，分类树对离散变量做决策树，回归树对连续变量做决策树。

预剪枝：它的位置在每一次生成分支节点前，先判断有没有必要生成，如没有必要，则停止划分。

后剪枝：先从训练集生成一棵完整的决策树（相当于结束位置），然后自底向上的对非叶结点进行考察。后剪枝时要用到一个测试数据集合，如果存在某个叶子剪去后能使得在测试集上的准确度或其他测度不降低（不变得更坏），则剪去该叶子。

image-20250313111522184

构建标准

在构建决策树时，我们需要选择最佳特征进行分割，常用的标准有以下几种：

1.信息增益（分类）

用于分类问题，衡量选择某一特征后数据集的纯度提升。通俗地说，它衡量的是用某个特征（比如“喜欢吃川菜”）划分数据后，关于目标（比如“喜欢吃辣”）的“混乱度”减少了多少。混乱度用“熵”（entropy）表示，熵越小越好。

信息增益 的计算公式为： $$ \text{信息增益} = \text{划分前熵} - \text{划分后熵} $$

2.增益比（分类）

是“信息增益的改进版”，它在信息增益的基础上，除以一个“固有信息”，让结果更平衡，防止偏向特征值多的特征。相当于考虑了复杂度。

增益比 的计算公式为： $$ \text{增益比} = \frac{\text{信息增益}}{\text{固有信息}} $$

3.基尼指数（分类）

衡量的是数据里 不同类别混在一起的“杂乱程度”，值越小说明类别越纯。想象你扔硬币猜正反面，猜错的概率越高，混乱就越大。

基尼指数 的计算公式为： $$ \text{基尼指数} = 1 - \sum_{i=1}^n p_i^2 $$ 其中，\(p_i\) 是第 \(i\) 类的概率。

4.均方误差（回归）

用于回归问题，衡量预测值与真实值之间的平均平方差，值越小说明预测越准。它把每个误差平方后求平均，大的错误会被“放大”处理。

均方误差 的计算公式为： $$ \text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 $$ 其中，\(y_i\) 是真实值，\(\hat{y}_i\) 是预测值，\(n\) 是样本数量。

框架

阶段名称 详细说明
Step 1 模型训练与验证
目标：训练决策树模型，并在测试集上进行评估。
评估标准：如果测试集准确率 ≥ 90%，则进入下一步。否则，调整参数重新训练。
Step 1.1 参数调整
目标：通过调整参数优化模型性能。
调整内容：如果模型准确率不达标，则修改以下参数重新训练：

- 最大树深度 (max_depth)
- 分裂标准 (criterion)
- 最小分裂样本数 (min_samples_split)
- 最小叶节点样本数 (min_samples_leaf)
Step 2 模型可视化
目标：用图表展示模型结构和重要信息，帮助理解决策过程。
主要内容：

1. 决策树结构图：展示树的分裂规则。
2. 特征重要性分析：找出影响决策的重要变量。
3. 混淆矩阵：分析分类错误情况。
4. 二维决策边界：显示不同类别的分布情况。
Step 3 最终结果
输出内容：经过训练和优化后的模型，附带完整的分析报告。

- 最终优化后的决策树模型
- 可视化分析报告
- 模型评估指标文档

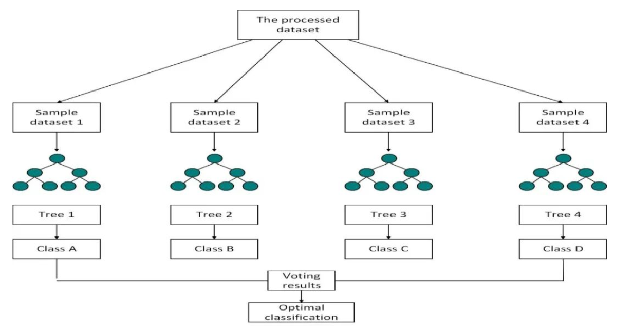
随机森林

随机森林（Random Forest）是一种基于决策树的 集成学习算法，由多个决策树组成的「森林」构成。它通过 Bagging（自助法采样）和特征随机选择 来提高模型的泛化能力，减少过拟合的可能性。该算法通常在分类问题和回归问题上都能取得良好效果。

对比维度 决策树 (Decision Tree) 随机森林 (Random Forest)
算法原理 构建一棵单独的树，基于特征分裂数据，形成层级结构 训练多棵决策树，并通过投票或平均值做最终预测
模型复杂度 较低，容易理解和解释 较高，由多个树组成，计算量大
准确性 可能对训练数据拟合过度，泛化能力较弱 由于多棵树投票，泛化能力更强，通常准确率更高
计算成本 训练和预测速度较快 由于需要训练多棵树，计算成本较高
抗过拟合能力 容易过拟合，尤其是深树 通过集成学习降低过拟合风险
特征重要性 可以提供特征重要性，但容易偏向某些特征 更稳定的特征重要性评估，不易偏向单一特征
适用场景 适用于简单、易解释的分类或回归任务 适用于需要高准确度和鲁棒性的任务，如金融、医疗预测等

原理分析

  • Bagging（自助法采样）

    在训练过程中，从数据集中 有放回地抽取 若干样本构建不同的决策树。每棵树只对一部分数据进行训练，使得模型更加稳健。 - 特征随机选择

    在每棵树的构建过程中，不是使用全部特征，而是 随机选择 一部分特征用于分裂节点，这进一步增强了模型的多样性。 - 多数投票和平均

    对于分类问题：多个树的预测结果通过投票决定最终类别。

    对于回归问题：将所有树的输出值取平均，作为最终预测值。

image-20250313113059030