数据

一、数据源推荐¶

比赛提供的数据 来源： 全国大学生统计建模大赛通常在赛题中 直接提供数据集，格式多为CSV、Excel或文本文件（如附件中的表格数据）。这些数据可能包含真实背景（如疫情数据、交通流量）或模拟数据。

特点： 数据通常具有实际意义，但可能存在缺失值、异常值或噪声，参赛团队需自行处理。

注意事项：

仔细阅读赛题说明，确认数据文件是否完整（例如，是否存在多个附件，如附件1、附件2）。检查数据 格式和字段含义，确保理解每个变量的定义。例如，字段“SiO2”表示二氧化硅含量，单位为百分比（%）。
公开数据集作为补充
- 国内平台：
中国国家统计局（http://www.stats.gov.cn）：提供宏观经济、人口、环境等统计数据。

中国开放数据平台（如天池、和鲸社区）：提供竞赛用数据集，如金融、医疗等领域的数据。
- 国际平台：
Kaggle（https://www.kaggle.com）：提供多种领域的公开数据集，如房价预测、医疗数据，常附带详细描述。

UCI Machine Learning Repository（https://archive.ics.uci.edu）：经典数据集，适合统计建模，如Iris数据集、Wine质量数据集。

World Bank Open Data（https://data.worldbank.org）：全球经济、环境、教育等数据。

使用场景： 比赛数据不足时，可用公开数据集补充。例如，若赛题涉及空气质量预测，但比赛数据缺少气象信息，可从中国国家统计局获取相关数据。

注意事项：

确保数据来源可靠，避免使用未经授权的数据。比赛通常不允许直接使用外部数据训练模型（如直接用Kaggle数据构建预测模型），但可作为参考或补充背景信息。

二、数据清洗实战¶

目标¶

确保数据质量，提高模型准确性：清洗后的数据应无缺失值、无异常值，格式统一，符合统计建模的要求。

提升模型可解释性：通过清洗去除噪声，确保分析结果符合实际背景。

常见问题及其处理方法¶

（1）缺失值处理¶

删除法：若缺失值比例较小（如<5%），可删除对应行。例如，df.dropna()。
填补法：均值/中位数填补：适用于数值型变量。
插值法：适用于时间序列数据，如df.interpolate()。
模型预测填补：使用KNN或随机森林预测缺失值（如sklearn.impute.KNNImputer）。
标记法：对于分类变量，可将缺失值标记为“未知”（如“颜色”字段缺失时，填入“未知”）。

实战案例：

数据（如SiO2列有10%缺失值），使用均值填补：f['SiO2'].fillna(df['SiO2'].mean(), inplace=True)。

论文中需说明填补方法及理由：“采用均值填补缺失值，因SiO2分布接近正态，且缺失比例仅为10%”。

（2）异常值检测与处理¶

IQR方法：计算四分位距（IQR），剔除超出范围的值（低于Q1-1.5IQR或高于Q3+1.5IQR）

Q1 = df['SiO2'].quantile(0.25)
Q3 = df['SiO2'].quantile(0.75)
IQR = Q3 - Q1
df = df[(df['SiO2'] >= Q1 - 1.5 * IQR) & (df['SiO2'] <= Q3 + 1.5 * IQR)]

物理约束：根据变量的物理意义剔除异常值。例如，化学成分含量应在0-100%之间，df = df[(df['SiO2'] >= 0) & (df['SiO2'] <= 100)]。
替换法：将异常值替换为均值或中位数。

（3）数据格式规范化¶

问题： 变量类型可能不一致（如“文物编号”可能是字符串或数值）、单位不统一（如百分比与小数混杂）。

统一变量类型：将字符串转为数值（如 df['文物编号'] = df['文物编号'].astype(int)）。

单位转换：确保所有化学成分均为百分比格式（如小数转为百分比：df['SiO2'] = df['SiO2'] * 100）。
时间格式处理：若涉及时间序列数据，统一格式（如pd.to_datetime(df['日期'])）。

实战案例：

附件中“文物编号”包含“部位”字样（如“03部位1”），提取数字部分：df['文物编号'] = df['文物采样点'].str.extract(r'(\d+)').astype(int)。

（4）变量筛选与特征工程¶

问题：

数据可能包含冗余变量（如高度相关的化学成分），影响模型性能。

相关性分析：

计算变量间的相关系数，剔除高度相关变量（相关系数>0.9）。以减少多重共线性。

corr_matrix = df[chemical_columns].corr().abs()
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(bool))
to_drop = [column for column in upper.columns if any(upper[column] > 0.9)]
df = df.drop(columns=to_drop)

数据清洗工具：

Python：pandas（数据处理）、numpy（数值计算）、matplotlib和seaborn（可视化）
R：dplyr（数据清洗）、ggplot2（可视化）

三、描述性统计分析¶

集中趋势分析¶

均值（MEAN）：反应总体水平
中位数（MEDIAN）：能够抗异常值影响
众数（MODE）：出现频率最高的值，适用于分类数据。

应用：如分析共享单车日均骑行次数的典型水平。

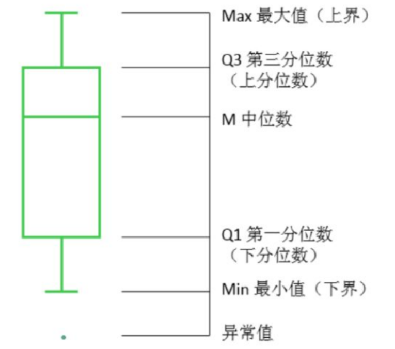
离散程度分析¶

方差（Variance）：数据偏离均值的平均平方差，衡量波动。
标准差（Standard Deviation）：方差的平方根，便于理解。
极差（Range）：最大值与最小值之差，简单但易受异常值影响。
四分位距（IQR）：第75百分位数（Q3）与第25百分位数之差，反映中间50%数据的分布。

应用：如评估骑行时间分布的离散程度。

分布形态分析¶

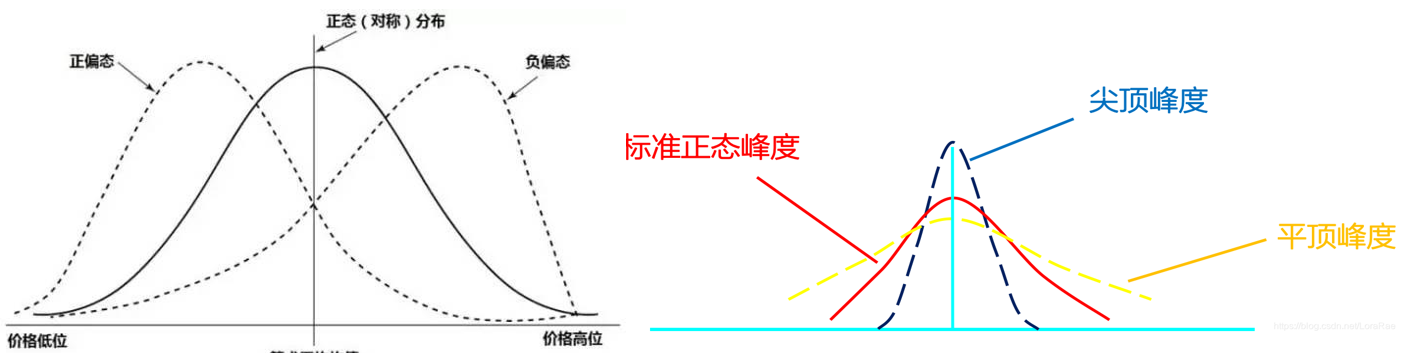
偏度（Skewness）：衡量数据分布的对称性。
- 计算：\(\(skew=\frac{ \sum(x_i-x)^3 / n}{s^3}\)\)
- 解释：正偏(右偏)、负偏(左偏)、对称。
峰度（Kurtosis）：衡量分布的陡峭程度。
- 计算：\(\(kurt =\frac{\sum\left(x_i-x\right)^4/n}{s^4} - 3\)\)
- 解释：尖峰(>0)，平峰(<0)，正态(≈0)。

工具：直方图、核密度图可视化分布形状。

应用：如判断气温数据是否偏态分布。

数据可视化¶

折线图、直方图、散点图、条形图、箱型图、其他图的融合

数据