PID

PID概念认知¶

概念¶

比例(Proportional)、积分(Integral)、微分(Derivative)

它是根据给定值（期望值）和实际输出值（当前值）构成控制偏差（误差），将偏差按比例、积分和微分通过线性组合构成控制量，对被控对象进行控制。

公式¶

\[ u(t) = K_p * e(t) + K_i * \int_{0}^{t}e(t) dt + K_d * \frac{d e(t)}{d t} \]

Kp：比例增益，用来调节反馈控制系统响应速度和稳定性。

增大Kp可以加快系统的响应速度，但可能导致系统震荡或超调；减小Kp则可能导致系统响应过慢。

输入偏差进行积分运算：直接与当前误差成比例，可以**快速响应误差的变化**，但容易导致系统振荡，会存在稳态误差。
Ki：积分增益，用来消除系统的稳态误差。

增大Ki可以减小系统的稳态误差，但可能导致系统的过度调节或振荡；减小Ki则可能导致系统无法消除稳态误差。

输入偏差进行积分运算：累积过去的误差，有助于消除静态误差，但可能导致系统响应缓慢或振荡。
Kd：微分增益，用来抑制系统的振荡和超调。

增大Kd可以减小系统的超调和振荡现象，但可能使系统对噪声和干扰更加敏感；减小Kd则可能导致系统的响应速度过慢。

输入偏差进行微分运算：预测误差的变化趋势，有助于减少系统的动态误差和振荡。
e(t)：误差信号，是期望值和实际值之间的偏差。

PID算法分类¶

基础
- 增量式
- 位置式
改进
- 积分分离
- 抗积分饱和
- 变速积分
- 死区控制
- 不完全微分
- ……

位置式PID¶

位置式PID控制通过比较实际输出和期望输出的差异，并根据误差的大小来调整控制输出。

位置式离散PID公式¶

\[ \int_{0}^{t}e(t) dt = (e_1 + e_2 + e_3 + … + e_i) * \Delta t $$ $$ \frac{d e(t)}{d t} = \frac{e_t - e_{t-1}}{\Delta t} \]

把 $\Delta t$ 合并到常数系数 K 中

\[ U_k = K_p \cdot e(k) + K_i \cdot \sum e(k) + K_d [e(k) - e(k-1)] \]

增量式PID¶

增量式PID控制不是直接使用误差值作为输入来计算控制输出，而是使用控制量的增量（即上一时刻和当前时刻的差值）作为输入。

\[ \Delta U_k = K_p [e(k) - e(k-1)] + K_i \cdot e(k) + K_d [e(k) - 2e(k-1) + e(k-2)] \]

给到控制器的输出值：

\[ u(t) = \Delta u + u(t-1) \]

位置式PID需要对积分项累加，适用于系统对稳态误差要求较高的场合。
增量式PID不需要对积分项累加，适用于系统对响应速度要求较高的场合。

串级PID¶

PID输出值的物理意义由输出值作用的地方决定

串级PID：将上一个PID控制器的输出量作为下一个PID控制器的输入量。

graph LR
    A[期望的位置] --> B[位置环PID控制器]
    B --> C[速度环PID控制器]
    C --> D[小车电机]
    D --> E[新位置]
    E --> |当前位置| B
    D -->|当前速度| C

通常而言，速度环比外环的位置环响应速度快3-5倍

单级与串级

单级
- 位置式PID可以让电机运转指定的圈数，但在运动过程中的速度控制相对较差。
- 增量式PID可以让电机运转指定的速度，但不直接控制电机的位置或角度。
串级
- PID内环：增量式PID，控制电机运转的速度
- PID外环：位置式PID，控制电机运转的距离/圈数

调参步骤

先单独调试速度环，使其具有良好的快速响应特性
再调整位置环参数，使其响应较慢但平稳
最后逐步优化两个路参数直至满足要求

平衡车的直立控制（PD）¶

物理分析¶

假设小车往右倾斜时，控制小车的车轮使小车作加速运动，加速度大小为 $a$。

受力分析示意图

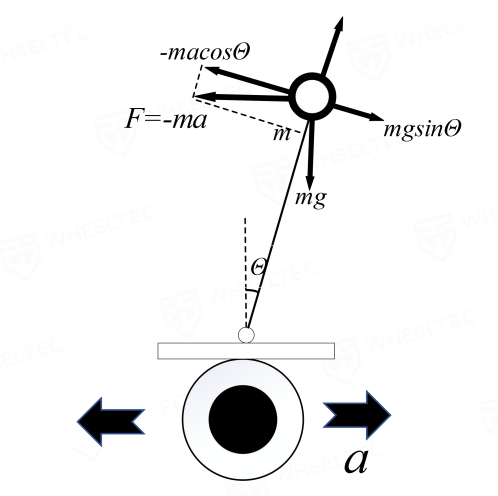
![image-20240812181107286](https://www.yahboom.com/public/upload/upload-html/1725878665/image-20240812181107286.png)

若以小车轮子为参考系（非惯性参考系）分析倒立摆受力，小车上方的圆球会受到一个方向与车轮加速度相反，大小与加速度成比例的惯性力。

$F=mgsin \theta - ma cos \theta \approx mg \theta - mk_1 \theta$ （$\theta$ 非常小 $\rightarrow sin \theta = 0,cos \theta=1$；$k_1$ 为加速度 $a$ 与小车倾角的比例系数）

若 $k_1 > g$，回复力的方向便与位移方向相反了。

而为了让倒立摆能够尽快回到垂直位置稳定下来，还需要增加阻尼力；增加的阻尼力与偏角的速度成正比，方向相反，因此公式可改为：

$F = mg\theta - mk_1\theta - mk_2\theta' = mg\theta - m(k_1\theta + k_2\theta')$（$k_2$ 为阻尼力与角速度的比例系数，$\theta'$为角度的微分（即角速度））

按照倒立摆的模型，可得出控制小车车轮加速度的算法：只要保证 $k_1 > g$，$k_2 > 0$ 就可以使小车平衡。

\[ a = k_1\theta + k_2\theta' \]

根据上述内容，建立速度的比例微分负反馈控制，使平衡车通过闭环控制保持稳定的条件。

通过MPU6050测量平衡车的倾斜角度θ和角加速度θ'，PD控制器根据测量到的倾斜角度和角加速度计算出控制信号，用于调整平衡车的速度，使车辆能够保持垂直立。

PD控制器¶

PID控制中微分（D）控制的主要作用是减少系统的动态误差和振荡，积分（I）控制的主要作用是消除静态误差。比例控制（P）可以快速达到设定的速度，微分（D）控制相当于阻尼力，可以有效抑制车模震荡。

实现代码¶

int Balance_PD(float Angle, float Gyro)
{
    float Angle_bias, Gyro_bias;
    int balance;
    Angle_bias = Mid_Angle - Angle; // 求出平衡的角度中值和机械相关
    Gyro_bias = 0 - Gyro;
    balance = -Balance_Kp / 100 * Angle_bias - Gyro_bias * Balance_Kd / 100; // 计算平衡控制的电机PWM PD控制 kp是P系数 kd是D系数

    return balance;
}

软件代码¶

平衡车PID控制基础：08-13教程只提供一个工程文件。

产品配套资料源码路径：附件 → 源码汇总 → 3.PID_Course → 08-13.Balanced_Car_PID

PID